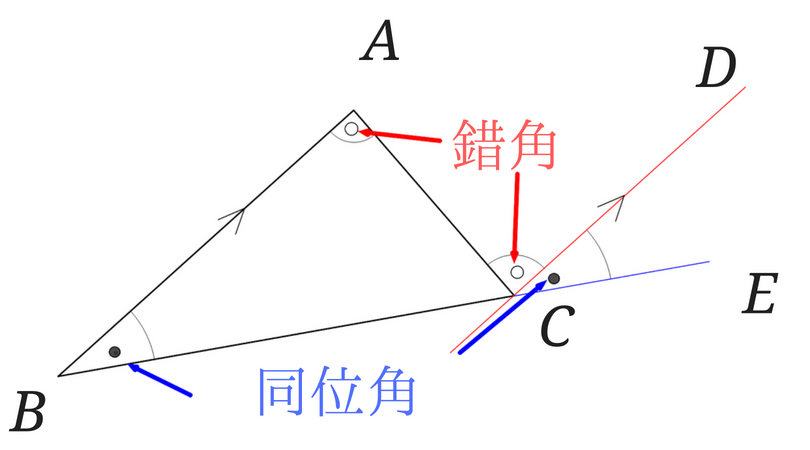
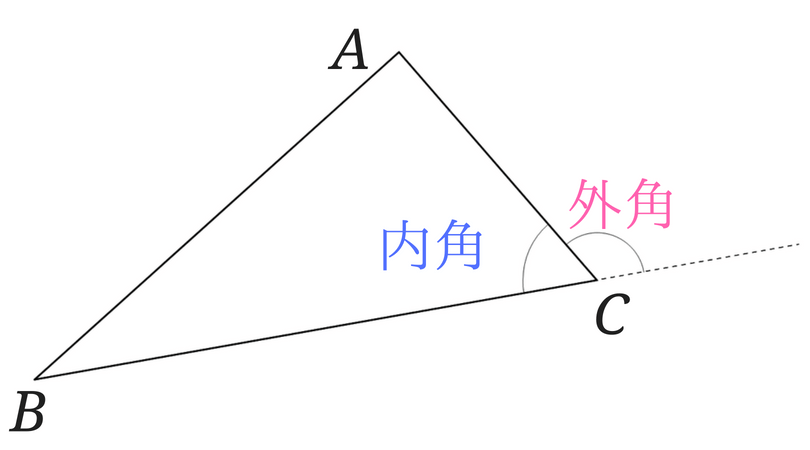
四角形に関する用語 対辺:繋がっていない(頂点を共有しない)辺のこと。四角形は2組の対辺を持つ(向かい合う辺)。 対頂点:辺を共有しない二頂点。四角形は2組の対頂点を持つ。 対角:対頂点における内角。 四角形は2組の対角を持つ(向かい合う角)。三角形の内角の和が180°になることの証明 三角形abcの内角をそれぞれ∠a、∠b、∠cとおく。 辺bcを点c側に延長して線分ceをひき、点cから辺baに平行な線分ceをひく。 そして∠ace=∠a'、∠ecd=∠b'とおく。ちなみに、四角形の内角の和は360°でしたね ∵ 四角形の内角の和 = abcdef = 2つの三角形の内角の和(abc)(def) = 180°×2 = 360° 同様に、 凹 ( おう ) 四角形の内角の和もちゃんと360°ですね 上の 凸 ( とつ ) 四角形同様、ちゃんと2つの三角形からでき

多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
四角形 内角の和 証明
四角形 内角の和 証明-・証明通し論理的筋道立推論し推論過程正しく表現うす ・各自画用紙四角形分度器内角の和求 ・作成した四角形の内角切取1点集内角の和 U r s四角形 p 360° t s こ q 確認す {期待さ生徒の姿 四角形内角 和360° た 演繹的推論 補助線2本引いたほう わやすいMixi小学校の先生 三角形の内角の和はなぜ180°なのか。 こんにちわ。 小学校教員3年目のあゆみと申します。 現在、5年生の担任をしております。 今、算数で「図形の角のひみつをしらべよう」という勉強をしているのですが、その中で子どもから出された1つの疑問に



内角の和と三角形の関係は 1分でわかる和の値 証明 外角との関係
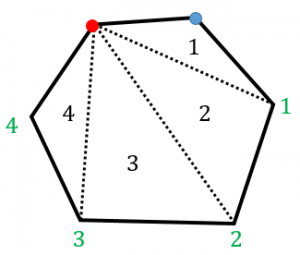
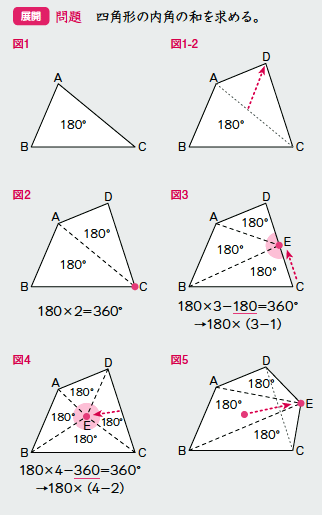
こんにちは、ウチダです。 今日は、中学2年生で詳しく学ぶ 「三角形の内角の和」 について、それが180度である証明や、三角形の外角に関する公式・問題を解説していきます。 また、記事の後半では「内角の和が270度である三角形」についても考察していきます。1. 図1で三角形の内角の和を確認する。図1-2の四角形を比較して角が一つ増えたことを確認。 2. 図1-2は二つの三角形から出来ていることから、四角形の内角の和が360°であることを確認する。 ※以前に習得した内容が強化される⑤ 三角形の外角 (証明) ⑥ 多角形の内角 (証明) n角形の対角線は、1つの頂点から、(n-3)本ひくことができる。 このことから、n角形は、(n-2)個の三角形に分割することができる。 n角形の内角の和は、(n-2)個の三角形の内角の和と同じなので
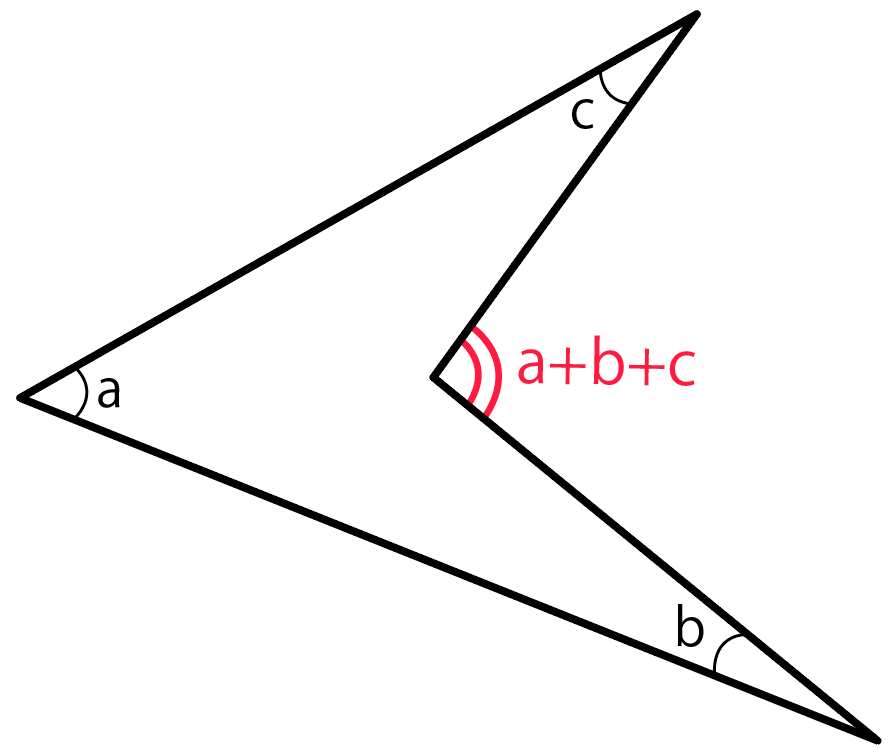
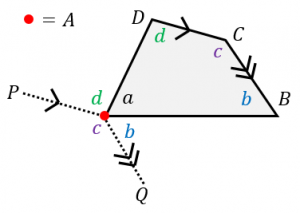
内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習になります。特徴 一般的には矢型、楔型などで呼ばれる。 四角形abcdにおいて、∠a,c,dの合計が角bの外角に等しくなる。 また、点bを中心とする円が点a,c,dに内接する場合、∠bの外角は∠dの2倍である。 証明 点d,点bを結び、∠bdcを∠f,∠cbdを∠l,∠bdaを∠h,∠abdを∠s,∠bの外角を∠xとすると、性質2五角形について, (4 つの内角の和) =(他の1 つの外周角)+180° すなわち,a+b+c+d=E+180° この性質の証明は,例えば,次に示す2 通り の方法が考えられる。 (証明1)五角形の内角の和を考えて, a+b+c+d+e=(5-2)×180°=540° ①
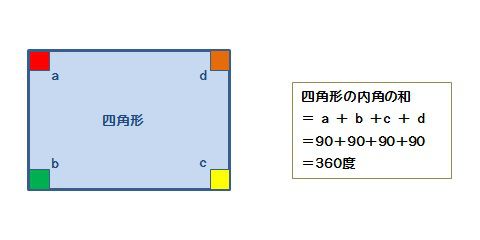
外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して 三角形の内角の和の証明がわからん?? こんにちは!この記事をかいているKenだよ。天満宮にいきたいね。 三角形の内角の和は「180°」になる って知ってた?? つまり、 中の角度をぜんぶ足すと180°になる 四角形の内角の和 四角形は 頂点 が4つで、 内角 と 外角 の対は4つあります。 すべての 内角 と 外角 の和は (a b c d) (A B C D) = 4 ⋅ 180 ∘ = 7 ∘



三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学
定理2.三角形の内角の和は 180度より小さい. (ア) 直角三角形の場合 直角三角形abc に対し,これと合同な三角形a'b'c' を作り,辺b'c を辺c' b に図のように重ね,四角形aba'cを作ります.このとき ∠=∠acb a bc′ ,∠=∠abc a cb′ . さらに線分bc の中点m をとり,m から直線ab に垂線mg を引き,課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を1 導入三角形・四角形の内角 の和、平行線と角 1 節 角 と 平 行 線 ①直線と角 対頂角の性質 平行線の性質 対頂角・同位角・錯角 ②三角形の角 2 三角形の内角と外角の性質 鋭角、直角、鈍角 内角の大きさによる三角形の分 類



内角の和と三角形の関係は 1分でわかる和の値 証明 外角との関係




多角形の内角の和 外角の和の公式 数学fun
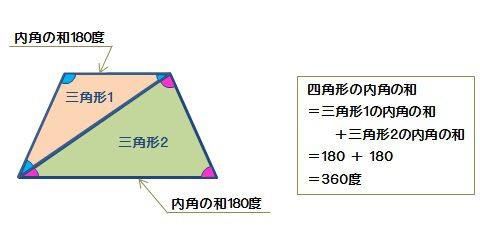
三角形の内角の和は180°であることを理解することができる。 多角形の内角の和を三角形の内角の和をもとにして求め、考え方を説明することができる。 4 評価規準 算数への 関心・意欲・態度 数学的な考え方 数量や図形についての 技能三角形の内角の和は180°だったよね? このことを利用して四角形の内角の和を調べよう。 一つの頂点から対角線を引いて、二つの三角形に 分けてみよう。三角形の3つの内角の和が180°であることは,小学校ですでに学習し,前時に証明している。四角 形,五角形の内角の和を自分なりの方法で求め,n角形の内角の和を求める公式を,単に暗記させるので 四角形の内角の和と求め方を確認させる。 五角形を




多角形の内角の和 外角の和の公式 数学fun



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
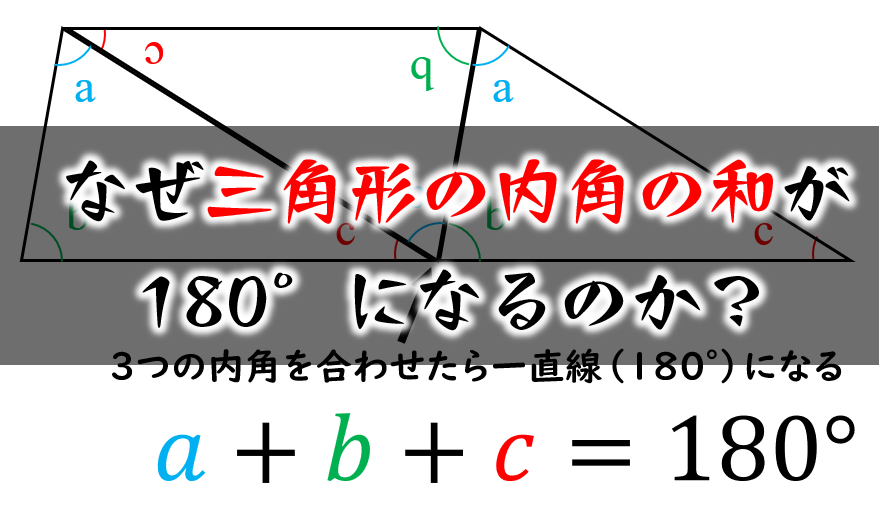
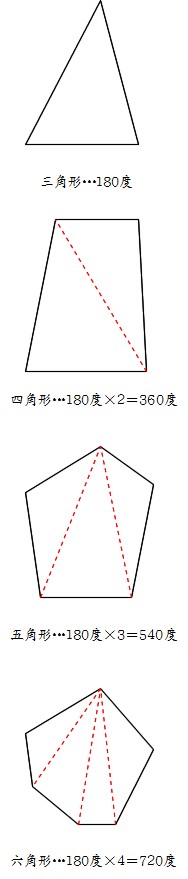
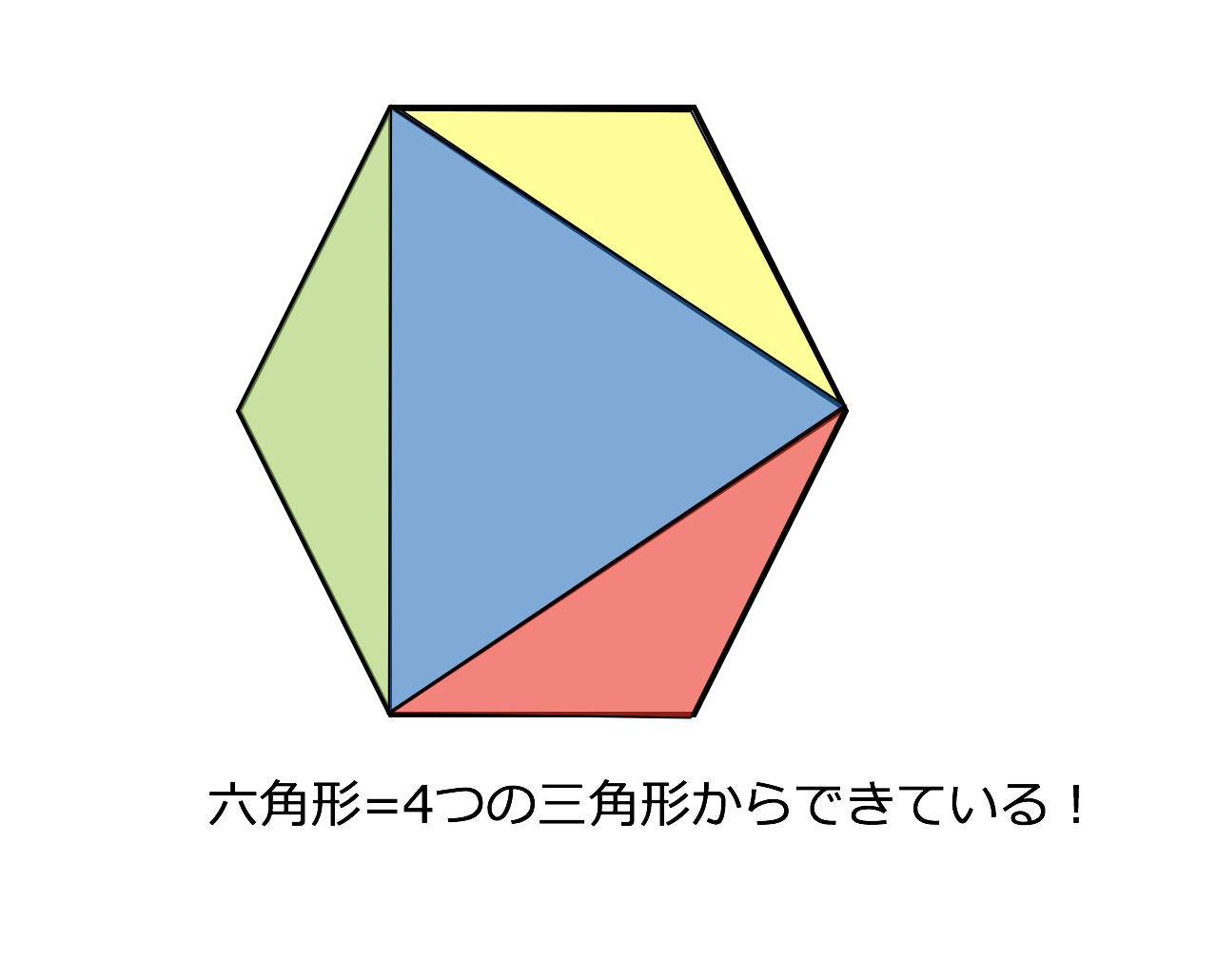
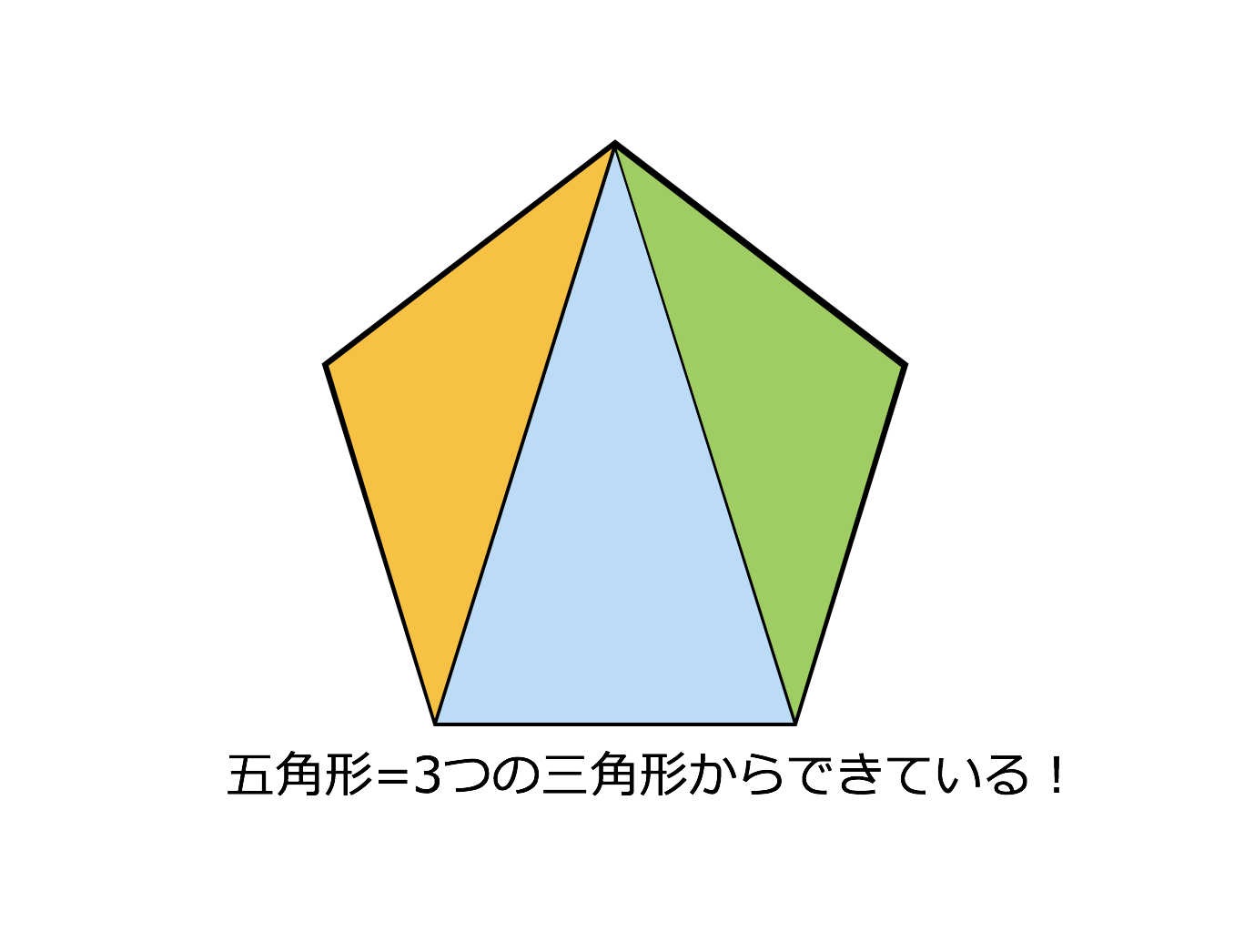
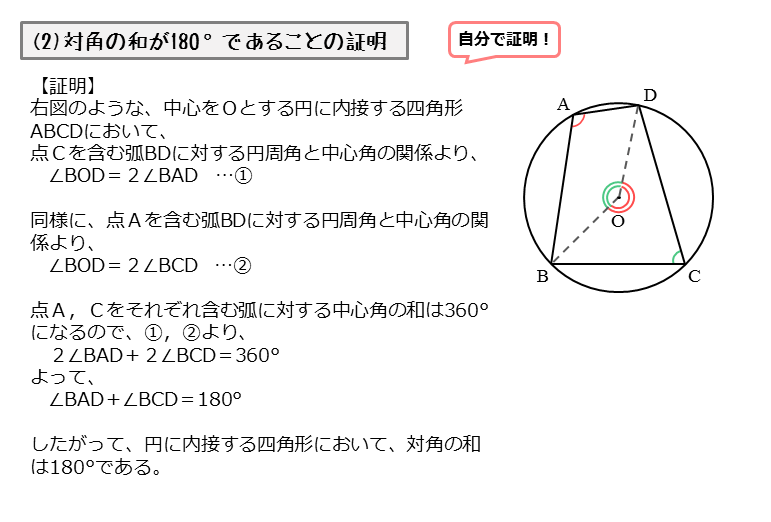
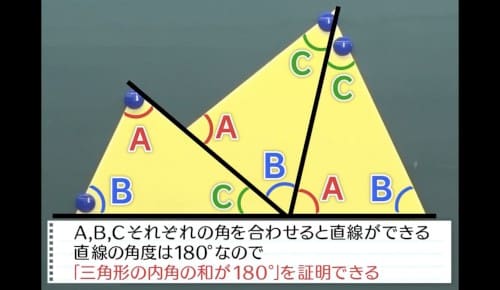
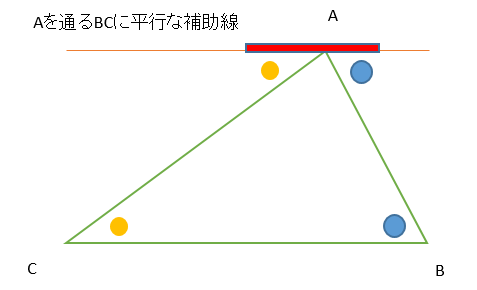
対角の和が180°である四角形は、円に内接する。 「円に内接する四角形の対角の和は180°である」 円に内接する四角形 数式で独楽する の逆の命題です。図を用いると、 四角形abcdについて∠a ∠c = 180°ならば、四角形abcdは円に内接する。 ということです。3点a, b, dを通る円を描四角形は三角形が2つ 五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\) これは忘れたら角度は求まりません。 多角形の内角の和の公式を表しこの説明だけでは「どんな三角形でも内角の和が\(180°\)になる」ということが証明できたわけではありません。 ただ、 「たしかに内角の和が\(180°\)になるみたいだ」 ということを子どもに理解してもらうには十分でしょう。実際にいろんな三角形を書いて



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun




至急 1問でもいいので教えて下さい よろしくお願いします Clear
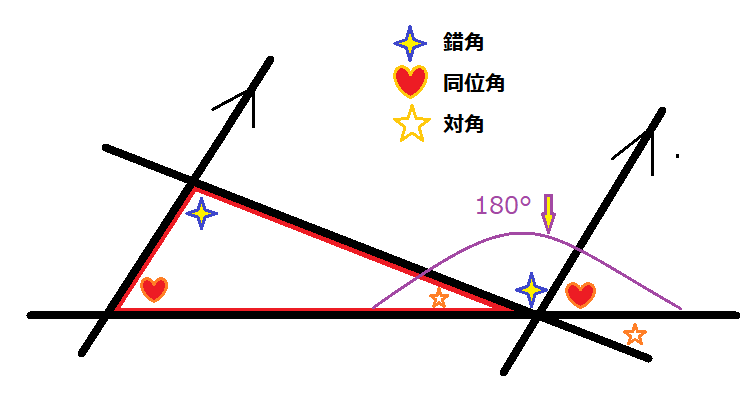
すべての三角形において 1辺が延長されるとき、 外角は二つの内対角の和に等しく、 三角形の三つの内角の和は2直角に等しい。 これが証明すべきことであった。 命題1ー32(三角形の内対角・内角の和) により、 命題1ー31(作図・平行線)さて,三角形の内角と外角について,次の重要な事実が成り立ちます. 三角形の内角と外角の性質: (1) 三角形の内角の和は $180°$ である. (2) 三角形の外角は,それと隣りあわない $2$ つの内角の和に等しい. これを証明してみましょう.(証明 2) 1つの三角形の内角の和は 180° 図6で示されるように, n角形は n−2 個の三角形に分けられるから,内角の和は (n−2)×180° 辺の数 3 4 5 n 形 三角形 四角形




四角形の内角の和 スクールプレゼンター教材共有サイト スクプレ道場



三角形の内角の和 180 の証明 こっけの備忘録
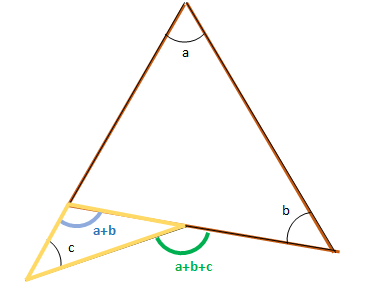
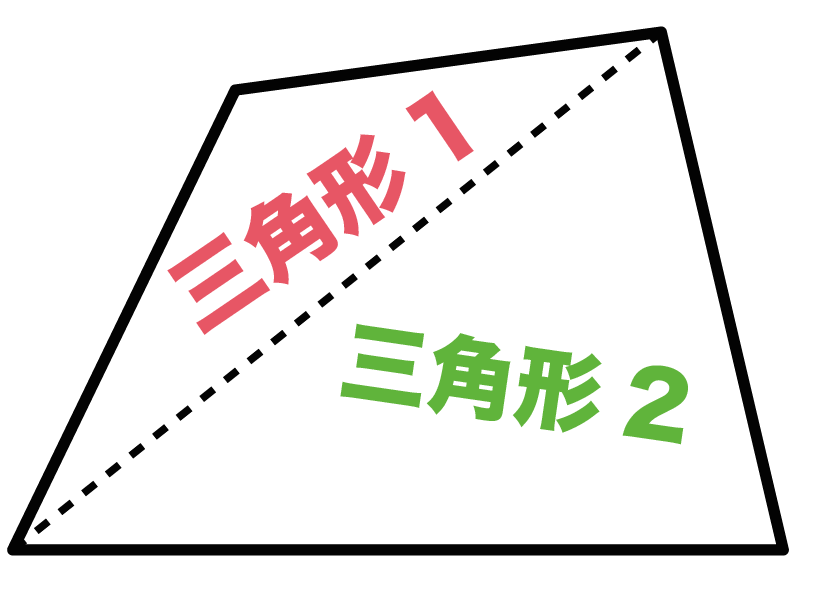
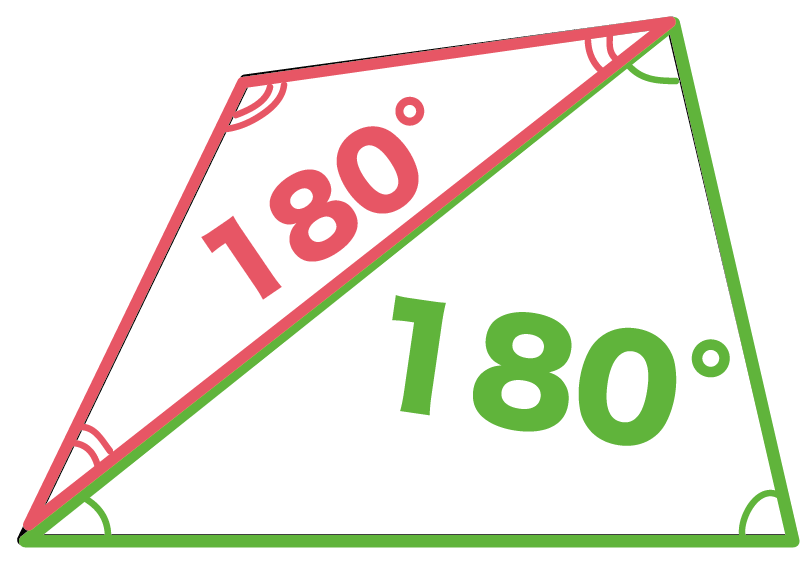
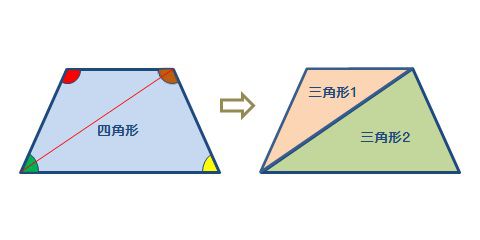
星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して三角形の内角の和が180度なのは知っていますよね? その三角形が2個あります。 つまり、 三角形1と三角形2の内角の和の合計が 四角形の内角の和 になるということ。したがって 四角形の内角の和=360度 となるのです。 だって、四角形の内角の和は360°だからさ。 このタイプの四角形を数学業界では、 長方形 ってよんでいるんだ。 2つの角がそれぞれ等しくてもダメ。 そいつは長方形なんかじゃない。 すべての角が等しくても、五角形じゃダメ。 長方形とは呼べないね。




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
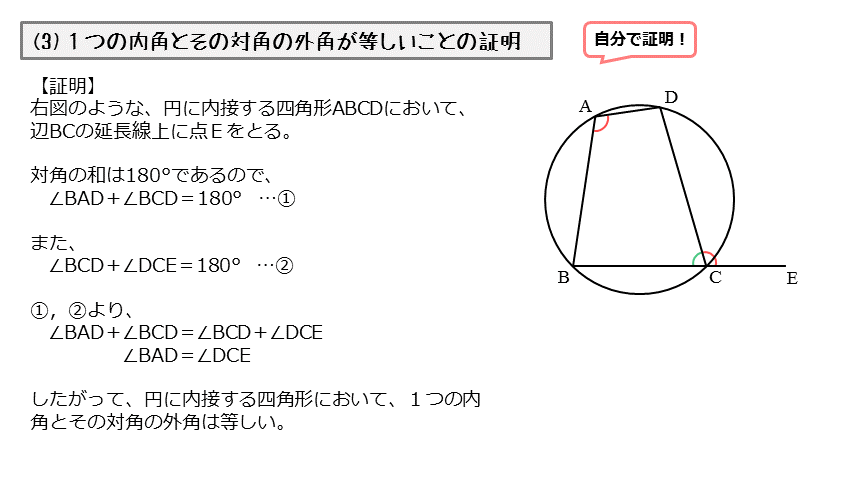



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん
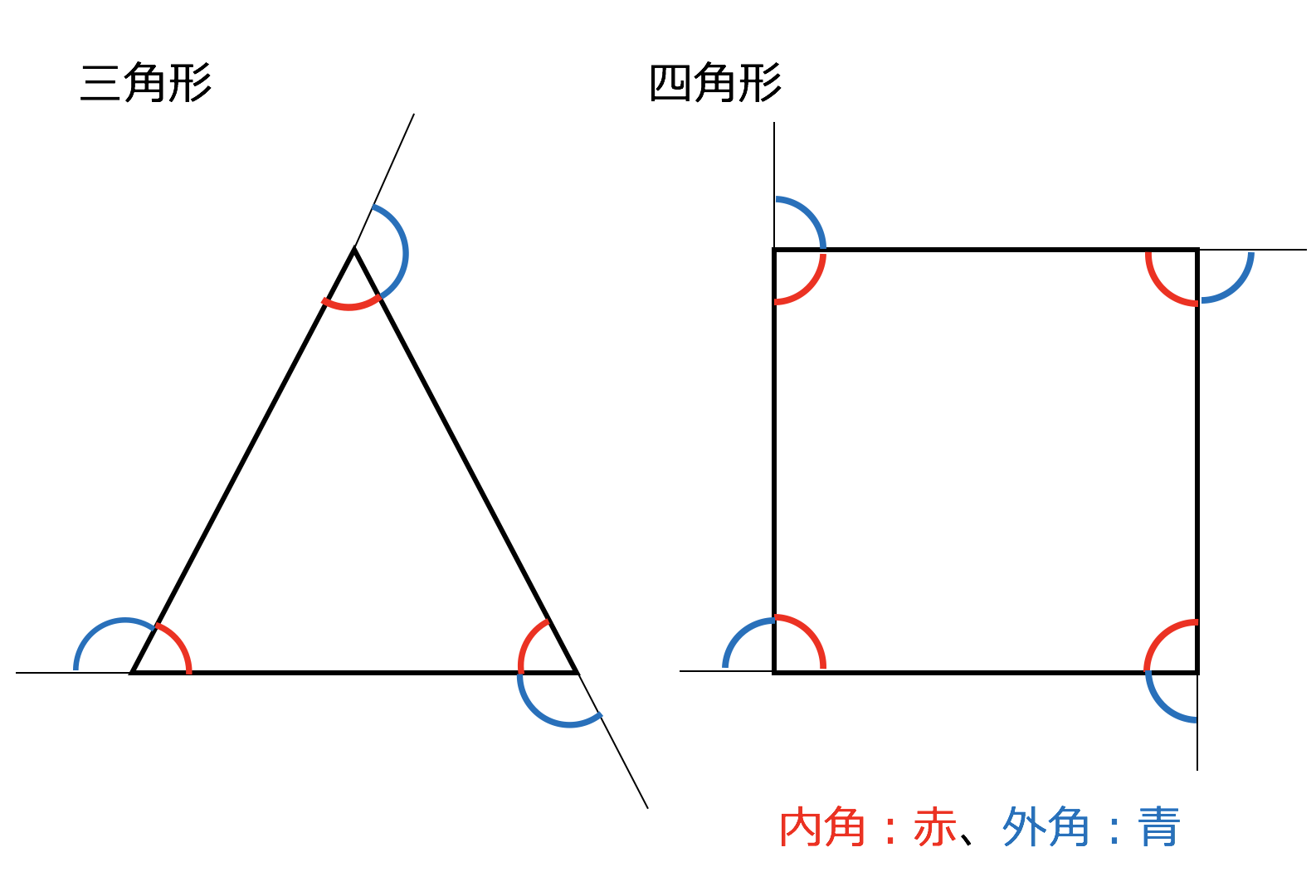
四角形ではそれが4組あるので、図の赤と青すべての角の和は180×4=7 青の角は内角なので四角形の内角の和360 赤と青の和7から青の和360を引くと7360=360 よって四角形の外角の和は360°となります。 同様のことを五角形でやってみると2次 ・三角形の内角の和が180°であることを証明する。 (1時間) ・三角形の内角と外角の関係を用いて三角形の内角や外角の大きさを 求める。 3次 ・印を付けた角の和を求める。 (3時間) 新B図形(1) イ平行線の性質や三角形の角についての性質を基に2nd grade 2年生は合同の証明や平行四辺形であることの証明など,論証をより深く学んでいきますね。 合同条件を見つけるなどパズルをはめていくようで楽しかったです。 三角形の内角の和は180°であることなど,図形の形を変えてもいつでもいえることの
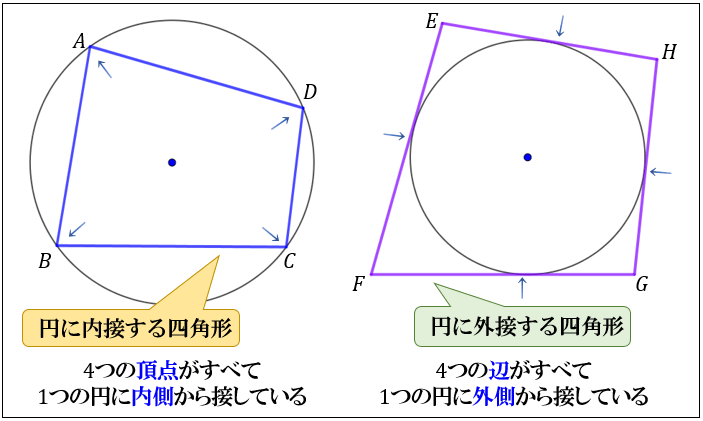



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



三角形の内角の和は180度以上になることはありえますか もし あるならば それはどんな場合ですか Quora
三角形の五心⑤ 三角形の傍心とその存在証明 スポンサーリンク 高校数学A 平面図形 検索用コード 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\ 2zh その交点を傍心は {1辺と他の2辺の延長からの距離が等しい点 向かい合う角の和は180° 円に内接する四角形における一番有名な性質です。 180^ {\circ} 180∘ である。 つまり, 性質1の逆も成立します。 つまり, 向かい合う内角の和が 180^ {\circ} 180∘ である四角形は円に内接します。 また,性質1は「外角」を使って→星形八角形を書いてみると、四角 形2つ分だから、確かに 180°増 えている。 →180°×(n4)になる。 ・黒板に残しておく。 ・星形五角形の次が無いか考えさせる。 その際、星形六角形や星形七角形 が出て くるよう誘導する。




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
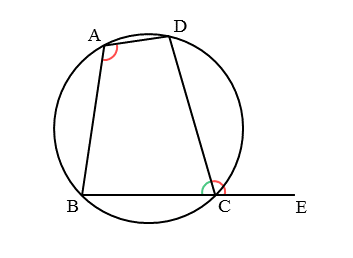



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん
した,三角形や 四角形の内角 の和を思い出 す。 「小学校では,三角形の3 つの角の和は何度になると 勉強してきたかな?」 三角形の内角の和を思い 起こす。 ⇒三角形の内角の和= 180゚ 「四角形の4つの角の和は 何度になるかな?」 四角形の内角の和が




中2 中2 数学 内角の和 授業ノート 中学生 数学のノート Clear




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




多角形の内角の和 外角の和の公式 数学fun



平行線と角度 7 ネット塾




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
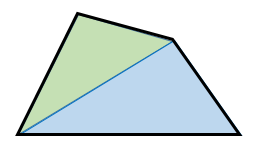



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学
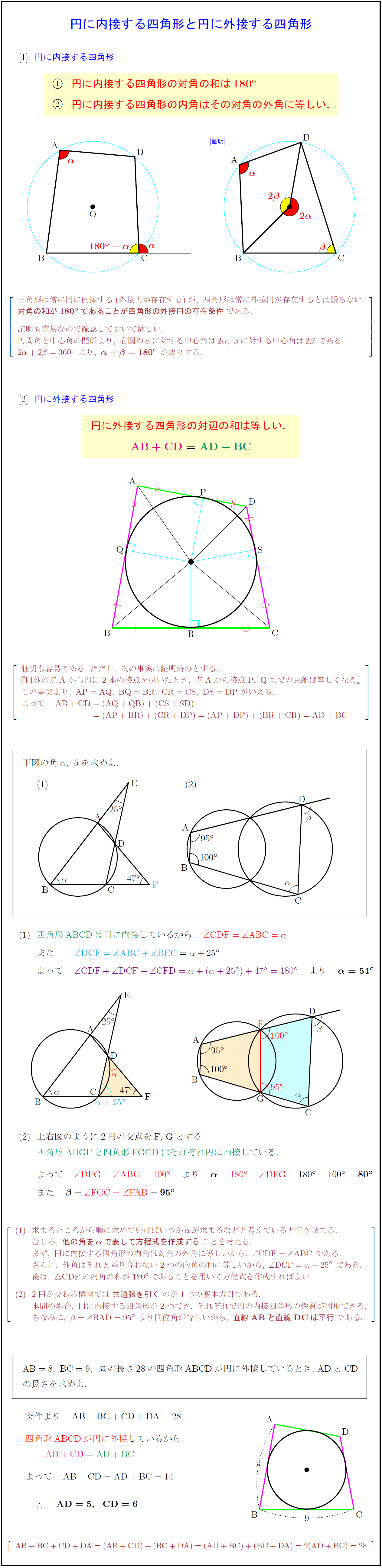



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月
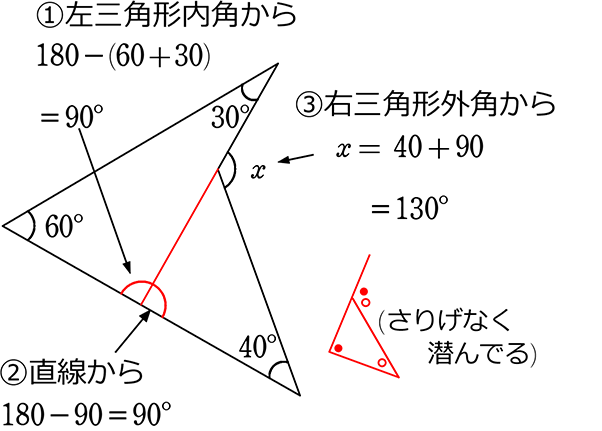



中学数学 平面図形と平行線の性質



Just For Today




多角形の内角の和の公式と外角の和を利用した角度の求め方




三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局



1




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
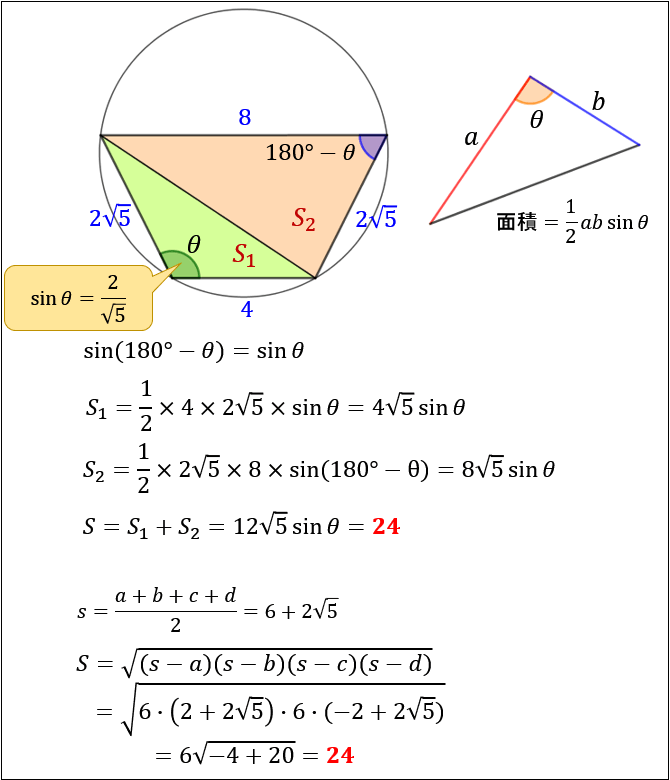



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
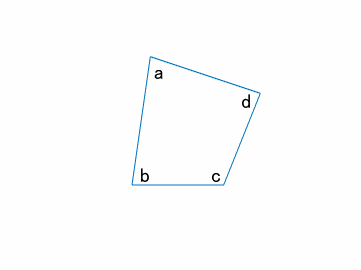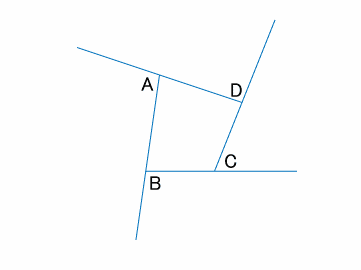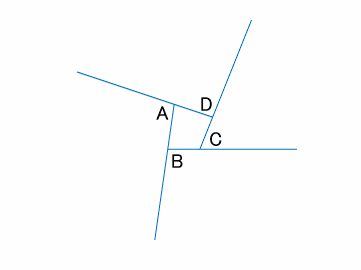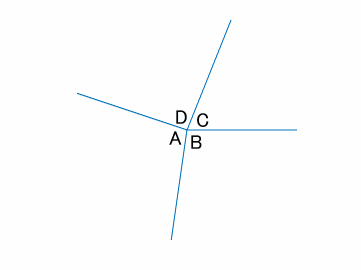



なぜ三角形の内角の和は180度 Qiita
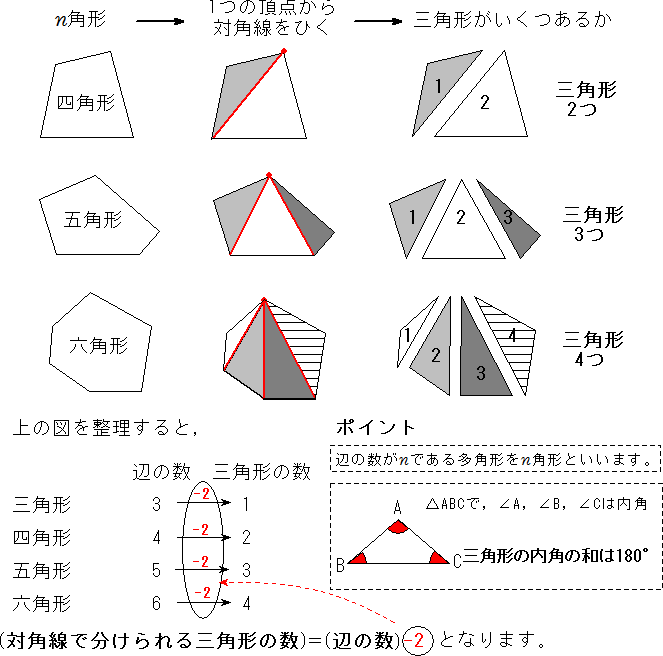



三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




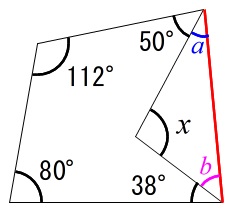
ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく



四角形の内角の和 算数の公式覚えてますか



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



Math 多角形の内角の和 働きアリ



ブーメランのような形をしている四角形 三角形 の内角の和は普通の四角形の内 Yahoo 知恵袋



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



1



1



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath



多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



なぜ三角形の内角の和は180度になるのですか Quora



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



2



四角形の内角の和 算数の公式覚えてますか




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




小学校5年 算数 四角形の内角の和 Youtube



図形の性質 円に内接する四角形について 日々是鍛錬 ひびこれたんれん



図の四角形abcdを用いて外角の和が360 になることを証明したいのです Yahoo 知恵袋



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



5年 三角形のふしぎ 算数イメージ動画集 大日本図書



中学数学円の中の四角形の向かい合う内角の和は 180度と習ったので Yahoo 知恵袋



Q Tbn And9gcs9bnffi742mzst0kt8 O6rcovhwzdtqw7lmxynruopks2brbc Usqp Cau




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




中学数学より1 星形5角形の内角の和 身勝手な主張




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




円に内接する四角形 証明 Youtube



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所



四角形の内角の和 算数の公式覚えてますか




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



多角形の内角の和の公式と外角の和を利用した角度の求め方
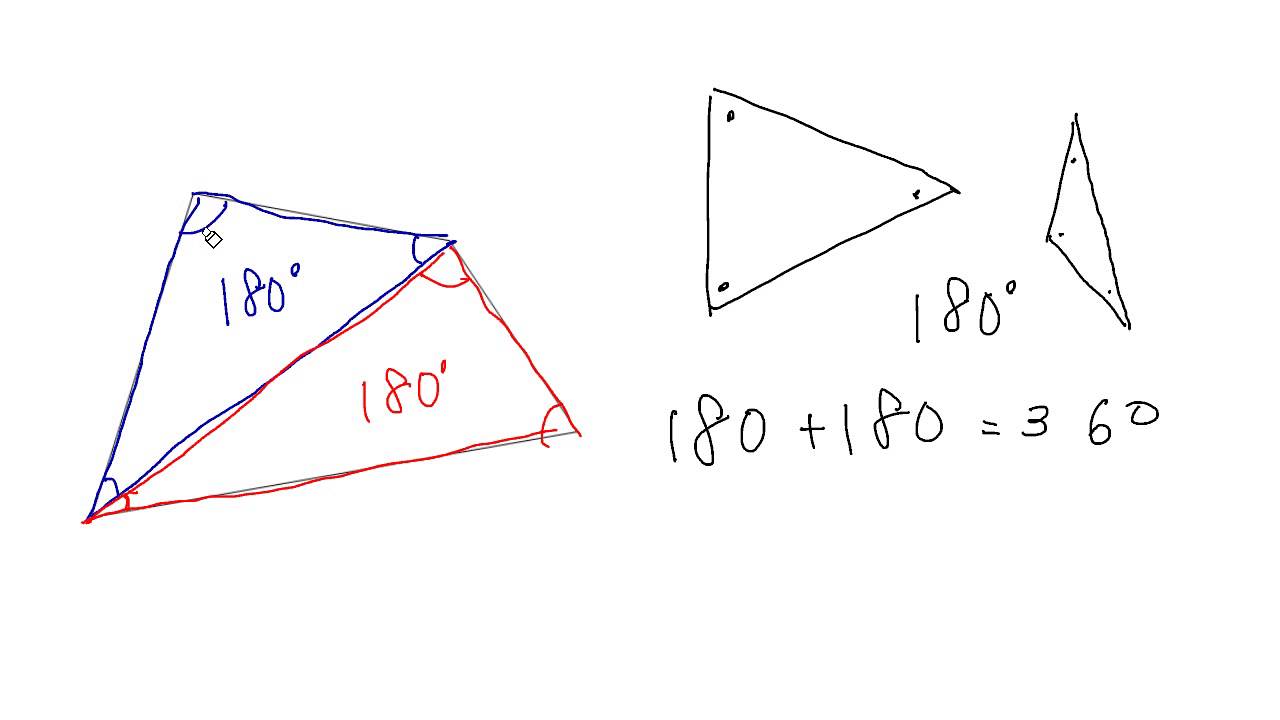



四角形の内角の和 Youtube



いろんな 角度 の話 ナイツ 松丸のサクッとスタディー 21 03 16 何ゴト



小学算数 幼稚園児でもわかる 三角形の内角の和 180度 の証明 偏差値40プログラマー




多角形の内角の和 算数の公式覚えてますか




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



多角形の内角と外角 思考力を鍛える数学




四角形の内角の和を求める問題で 四角形に 三角形を上に足して求める方法が理解 Clear




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




多角形の内角の和 外角の和の公式 数学fun




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




小学校5年 算数 四角形の内角の和 Youtube




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




中2数学 ブーメラン型角度の求め方を解説 数スタ




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
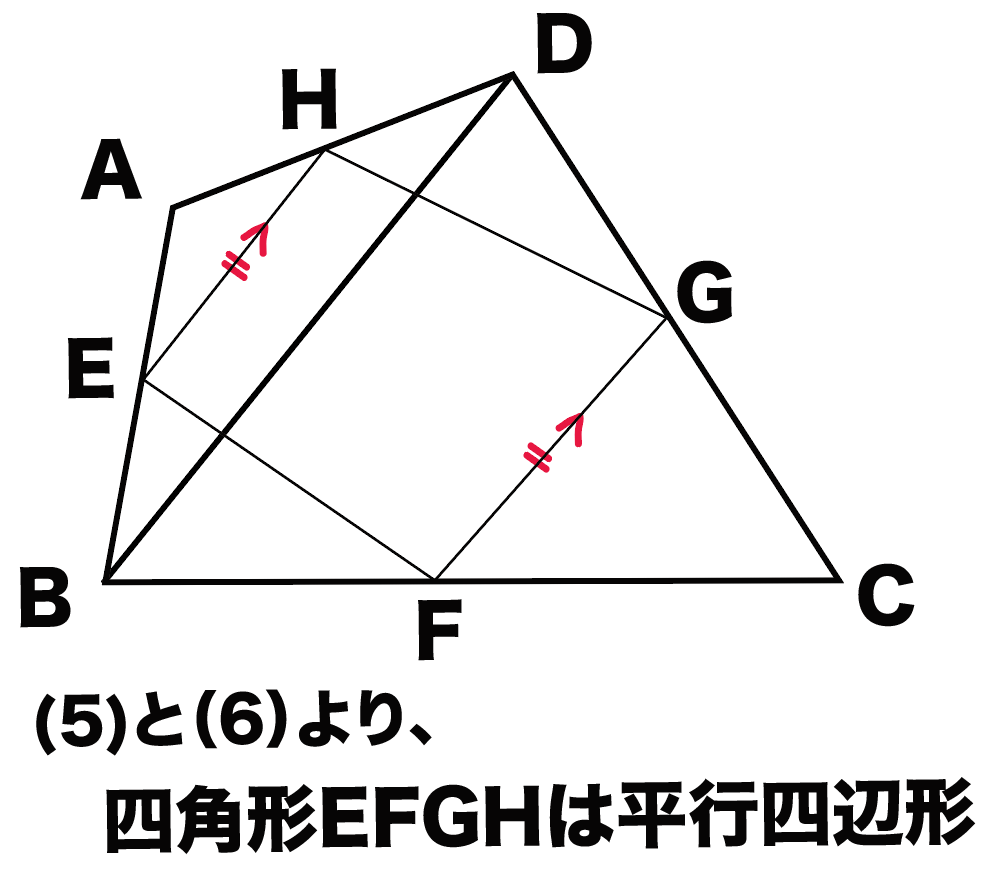



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく
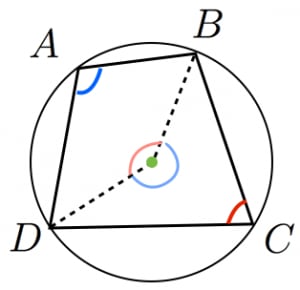



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語
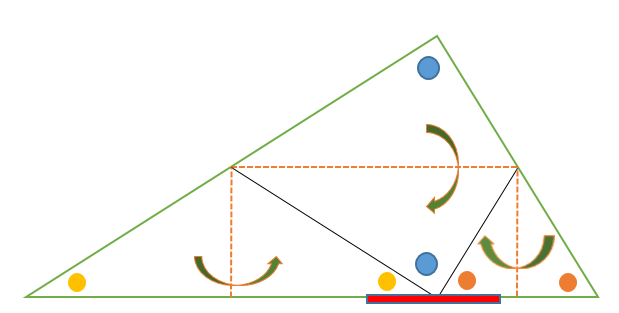



小学算数 幼稚園児でもわかる 三角形の内角の和 180度 の証明 偏差値40プログラマー




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



四角形についてですが ブーメラン型の四角形も内角の和は360 Yahoo 知恵袋




円に内接する四角形の対面にある内角の和は180 という定理の逆はなり 数学 教えて Goo




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア
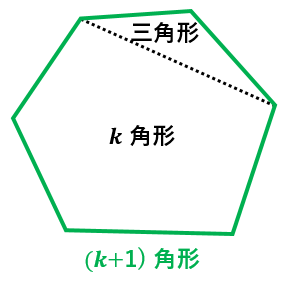



多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
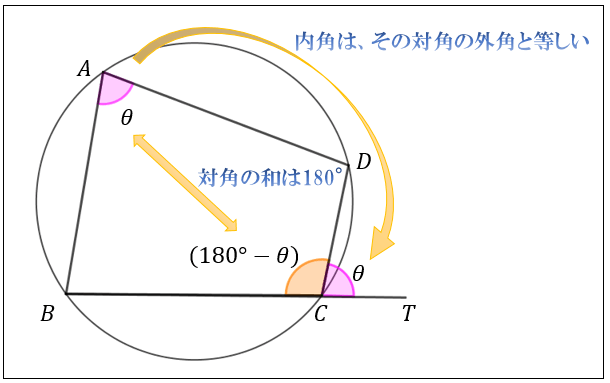



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



0 件のコメント:
コメントを投稿